I really need to get a publicist. This post should have gone up at the end of November, not December.

In the run up to the winter solstice this year (2019), and for the day beforehand and for the day itself, there was a lot of confusion on twitter (well … more confusion on twitter than is normal anyway) as to whether and why the winter solstice fell on the 22nd December, and not – as we were all assuredly taught in school – on the 21st. I replied on a few occasions, but I'm putting this post together as a reference on the subject¹.

To start, we need to note this most important fact:

It takes 365.24219 days for the earth to go around the sun, what we call a year².

That's not exactly 365 days. It's nearly 365 and one quarter days. That means that the earth kind-of gains a quarter of a day over the calendar every year. Or one day every 4 years. Which is why we add a day every four years.

The following graph shows the dates and times of the moments of the equinoctes³ and solstices for the next 50 years. They all happen between the 00:01 of 19th of the month (March and September for the equinoctes; June and December for the solstices) and very early in the 24th of the month.

By "moment", I mean one of the following:

• For the equinoctes, it's the moment that the sun is exactly over the equator as it passes from the northern hemisphere to the southern (in September) or from the southern to the northern (in March).
• For the solstices, it's the moment that the sun is directly over the most northern latitude that it can be (June) or the most southern latitude (December).

The day of the solstice or equinox is the day in which this "moment" occurs. For the purpose of this blog post, we're showing the moment at Dublin time.

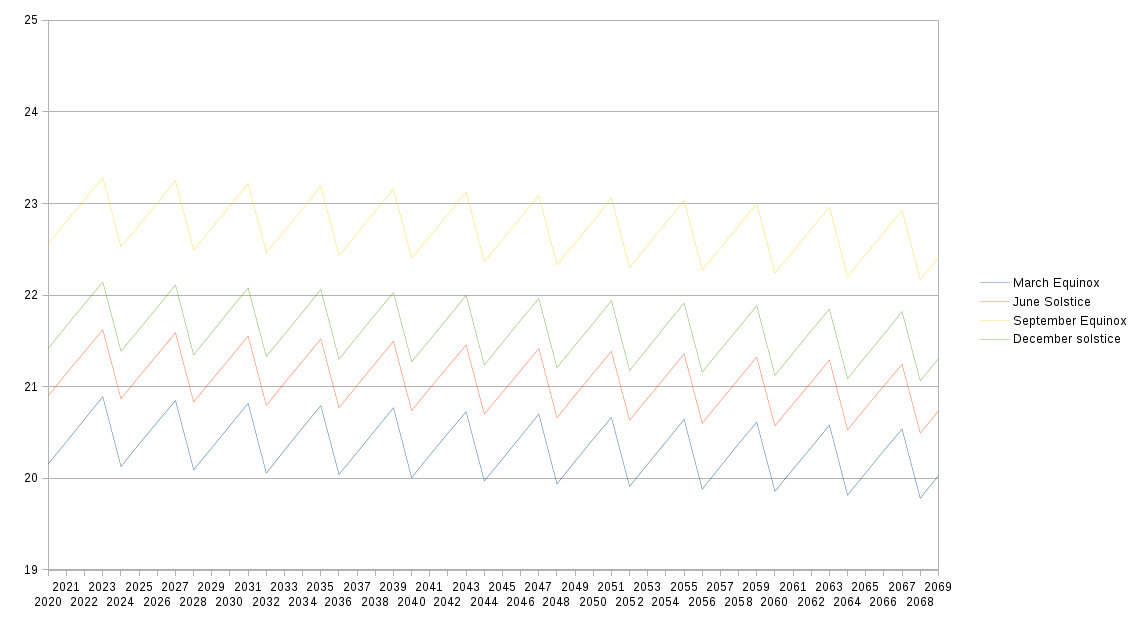
You can see that the moment of each of the solstices and equinoctes progress forward for 4 years, and then is abruptly pulled back for the next 4 years.

Some interesting points: The "traditional" date for the December solstice, the 21st December, holds true most of the time. It creeps into the 22nd in 2023, 2027, 2031, 2035, 2039 and 2043, but stay firmly in the 21st for all other years. Each of those years is immediately before a leap year, when the calendar is reset. We also see that the September equinox is more often than not in the 22nd September, but sometimes (in years immediately before leap years) in the 23rd. The June solstice quite evenly shares the 20th and the 21st, though the trend clearly favours the 20th, and the March equinox takes place most of the time on the 20th.

And … to state it explicitly, these times are getting earlier over the 50 years.

This is because a year is 0.24219 days longer than 365 days, and not an exact 0.25 days. As a result, adding an extra day every 4 years is an over-correction, and if this was to continue, we'd be celebrating the March equinox in February!

Therefore, the rule is that if the year can be evenly divided by 4, it's a leap year, unless it can be evenly divided by 100, in which case it isn't a leap year. So the over-correction of adding an extra day every 4 years is mitigated by not adding it every 100 years.

However, the correction of the over-correction is, itself, an over-correction, so there's another finesse to the formula: if the year is evenly divisible by 4 it's a leap year unless it can be divided evenly by 100, in which case it's not a leap year, unless it can be divided evenly by 400, in which case it is a leap year.

Thus, 2000 was a leap year, but neither of 1900 nor 1800 were, nor will any of 2100, 2200 nor 2300. But 2400 will be a leap year.

If we extend the above graph to cover the equinoctes and solstices for the next 500 years, we see that in effect:

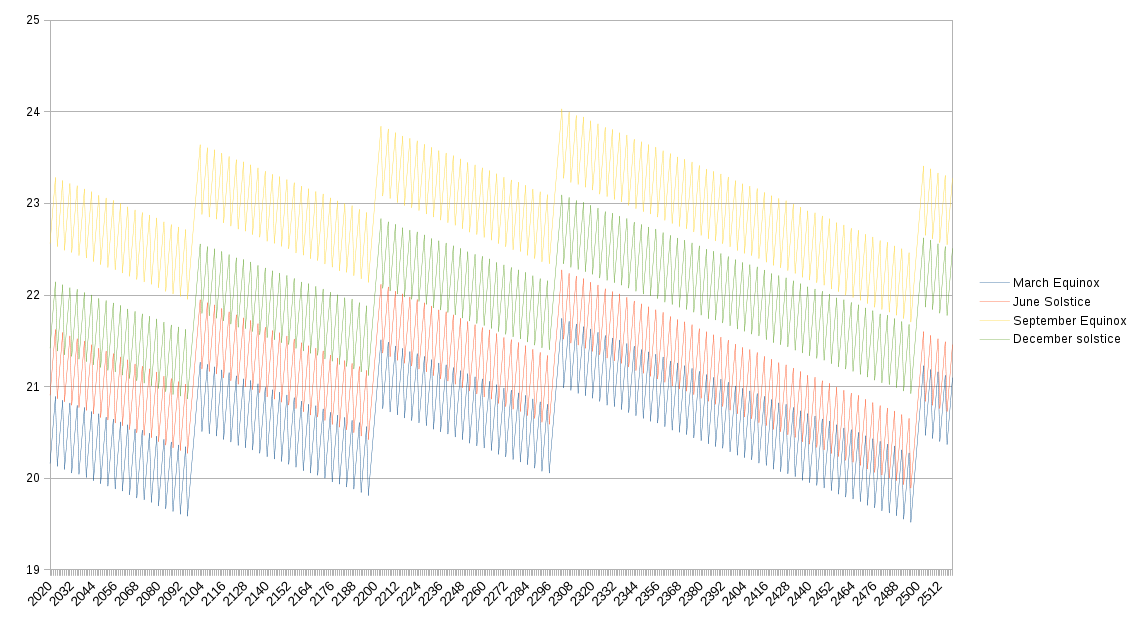
Here you can see there isn't a resetting of the dates in 2100, 2200 or 2300, but there is in 2400, which seems to bring the times of the equinoctes and solstices back to where the are at the beginning of this century.

When we look at the times for the next 1000 years, we see it more clearly, as it shows how there 2400 and 2800 are leap years when the other '00 years aren't:

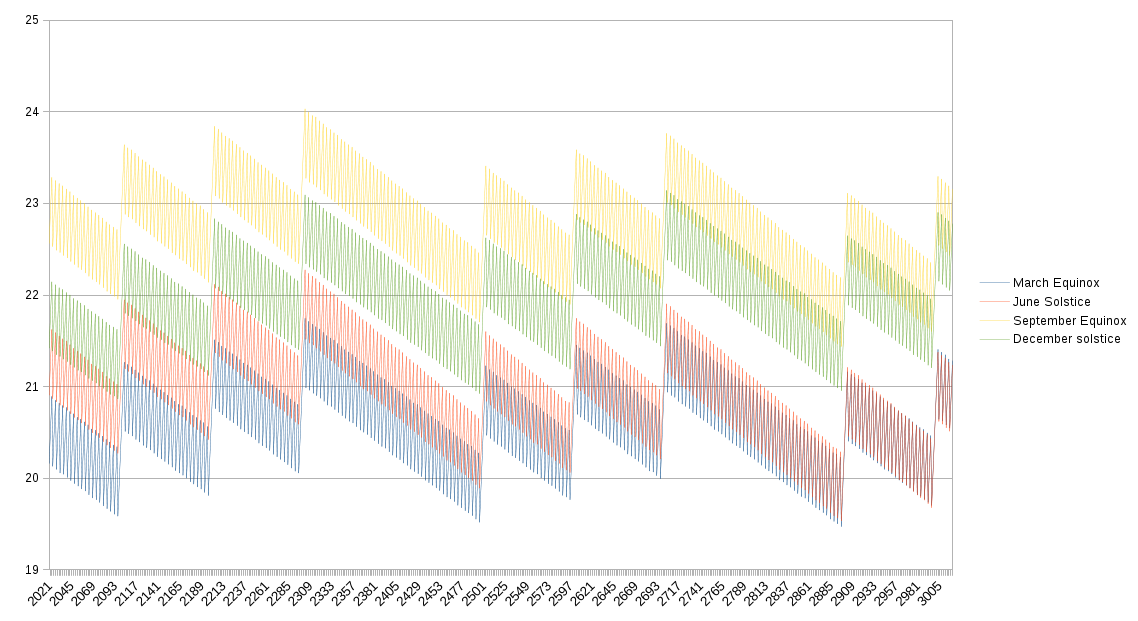
I don't have an explanation, however, for how the times don't remain constant relative to each other over those 1000 years. If you look closely – even with the corrections on the leap years – the time of the June solstice is trending earlier over the period, whereas the time of the March equinox seems to be trending ever-so-slightly later. Similarly, the time of the September equinox is trending earlier while the time of the December solstice trends later.

The software I used to create these graphs is the solar package that comes as standard with the GNU/Emacs software, and the following caveat is offered in the code:

;; Accuracy:
;;    1. Sunrise/sunset times will be accurate to the minute for years
;;       1951--2050.  For other years the times will be within +/- 2 minutes.
;;
;;    2. Equinox/solstice times will be accurate to the minute for years
;;       1951--2050.  For other years the times will be within +/- 1 minute.

There could be something interesting going on with how these astronomical phenomena occur, or it could simply be that the software can't handle dates greater than 2050. I'm inclined to think the latter.

If you know what's going on, let me know, and I'll update this blog post with the details.

The data for these graphs can be accessed here.

---